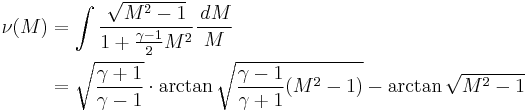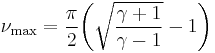Prandtl–Meyer function

Prandtl–Meyer function describes the angle through which a flow can turn isentropically for the given initial and final Mach number. It is the maximum angle through which a sonic (M = 1) flow can be turned around a convex corner. For an ideal gas, it is expressed as follows,

\begin{align} \nu(M) & = \int \frac{\sqrt{M^2-1}}{1%2B\frac{\gamma -1}{2}M^2}\frac{\,dM}{M} \\ & = \sqrt{\frac{\gamma %2B 1}{\gamma -1}} \cdot \arctan \sqrt{\frac{\gamma -1}{\gamma %2B1} (M^2 -1)} - \arctan \sqrt{M^2 -1} \\ \end{align}

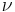where, \nu \, is the Prandtl–Meyer function, M is the Mach number of the flow and \gamma is the ratio of the specific heat capacities.

By convention, the constant of integration is selected such that 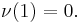\nu(1) = 0. \,

As Mach number varies from 1 to 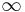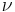\infty, \nu \, takes values from 0 to 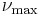\nu_\text{max} \,, where

\nu_\text{max} = \frac{\pi}{2} \bigg( \sqrt{\frac{\gamma%2B1}{\gamma-1}} -1 \bigg)
For isentropic expansion, 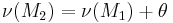\nu(M_2) = \nu(M_1) %2B \theta \,
For isentropic compression, 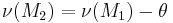\nu(M_2) = \nu(M_1) - \theta \,

where, \theta is the absolute value of the angle through which the flow turns, M is the flow Mach number and the suffixes "1" and "2" denote the initial and final conditions respectively.

See also

References